Glory Info About Where Is The Least Squares Or Best Fitting Line Gaussian Distribution Excel Graph

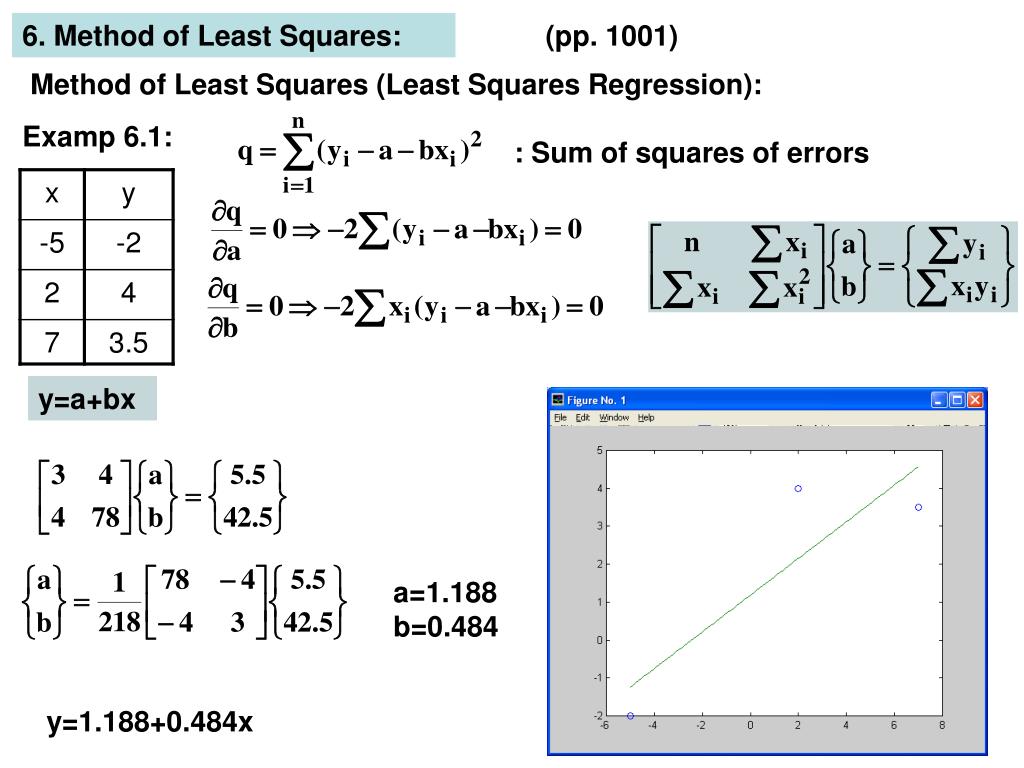
Use the least square approximation to find the closest line (the line of best fit) to the points:

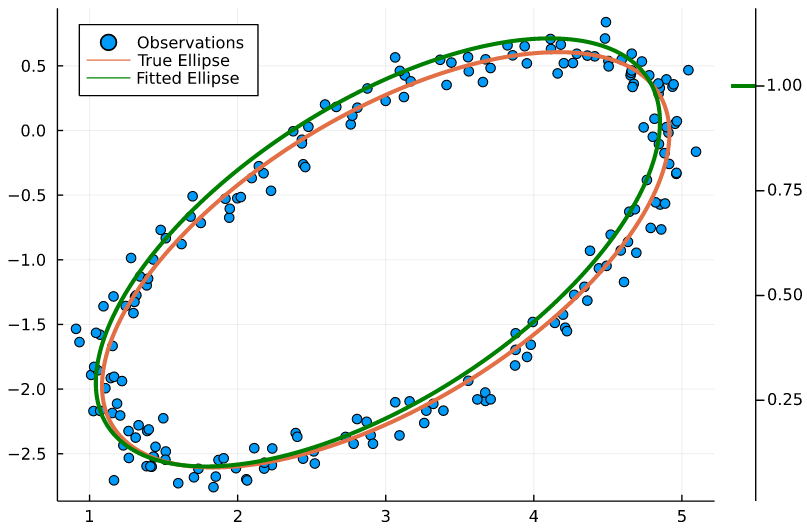
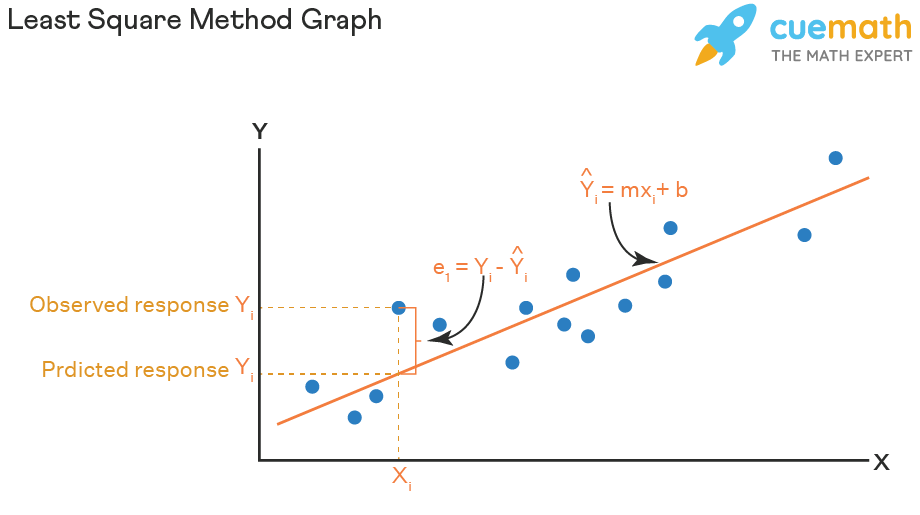
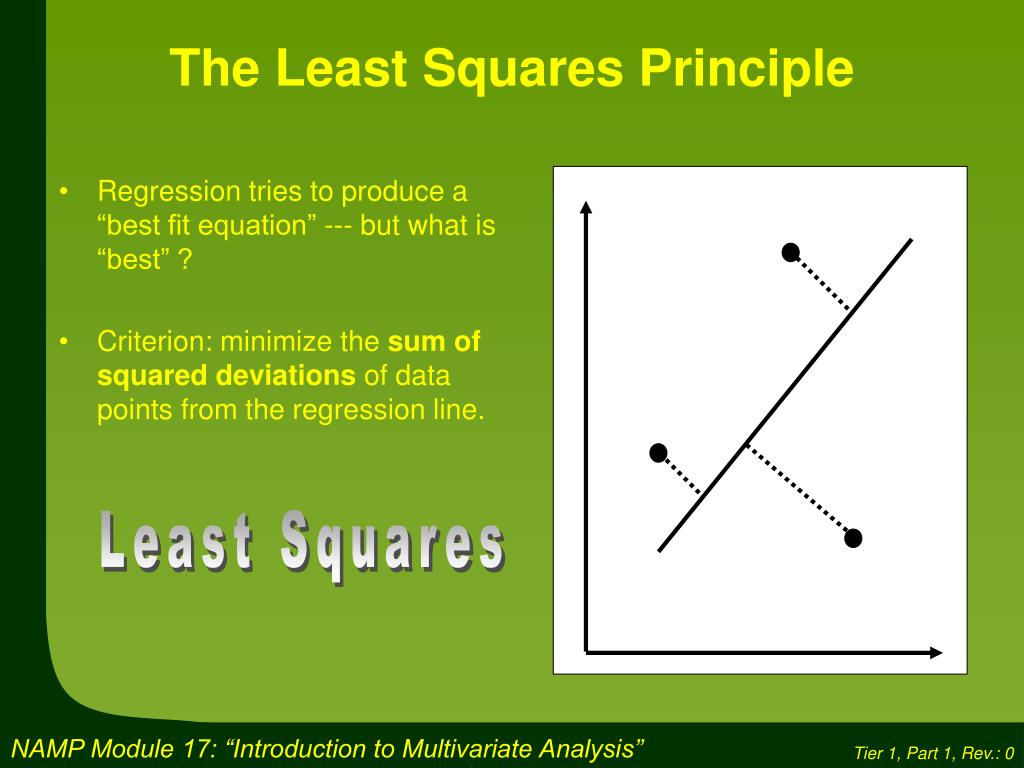
Where is the least squares or best fitting line. The method of least squares is a parameter estimation method in regression analysis based on minimizing the sum of the squares of the residuals (a residual being the difference between an observed value and the fitted value provided by a model) made in the results of each individual equation. Unlike the standard ratio, which can deal only with one pair of numbers at once, this least squares regression line calculator shows you how to find the least square regression line for multiple data points. In a previous post, i introduced the theory behind the method of least squares and showed how it can be used to solve systems of equations with no unique solution.

We just need to find the values b0 and b1 that make the sum of the squared prediction errors the smallest it can be. Atax =atb a t a x = a t b. Q = ∑ i = 1 n ( y i − y ^ i) 2.

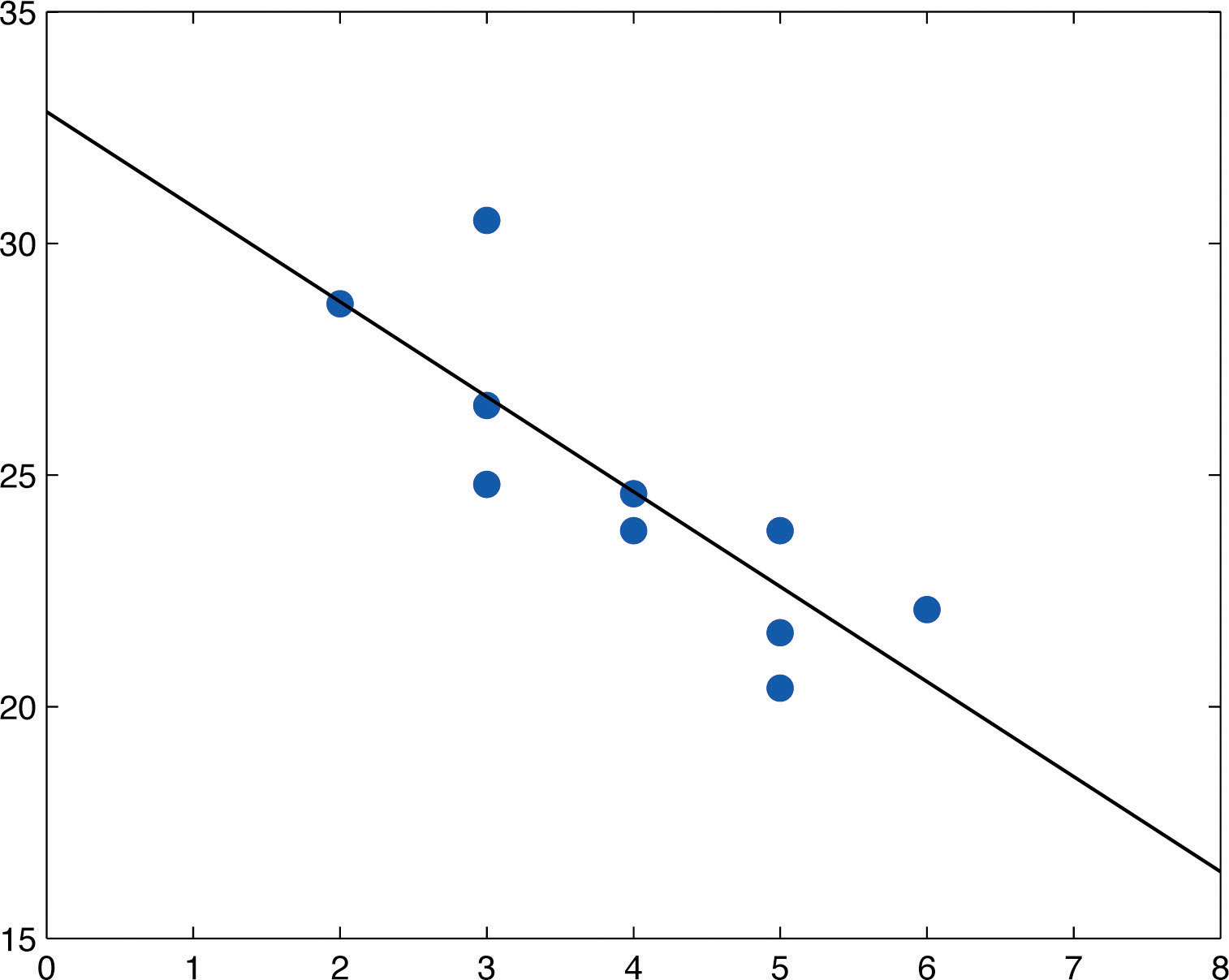
It is called the least squares regression line. We can place the line by eye: That is, we need to find the values b 0 and b 1 that minimize:

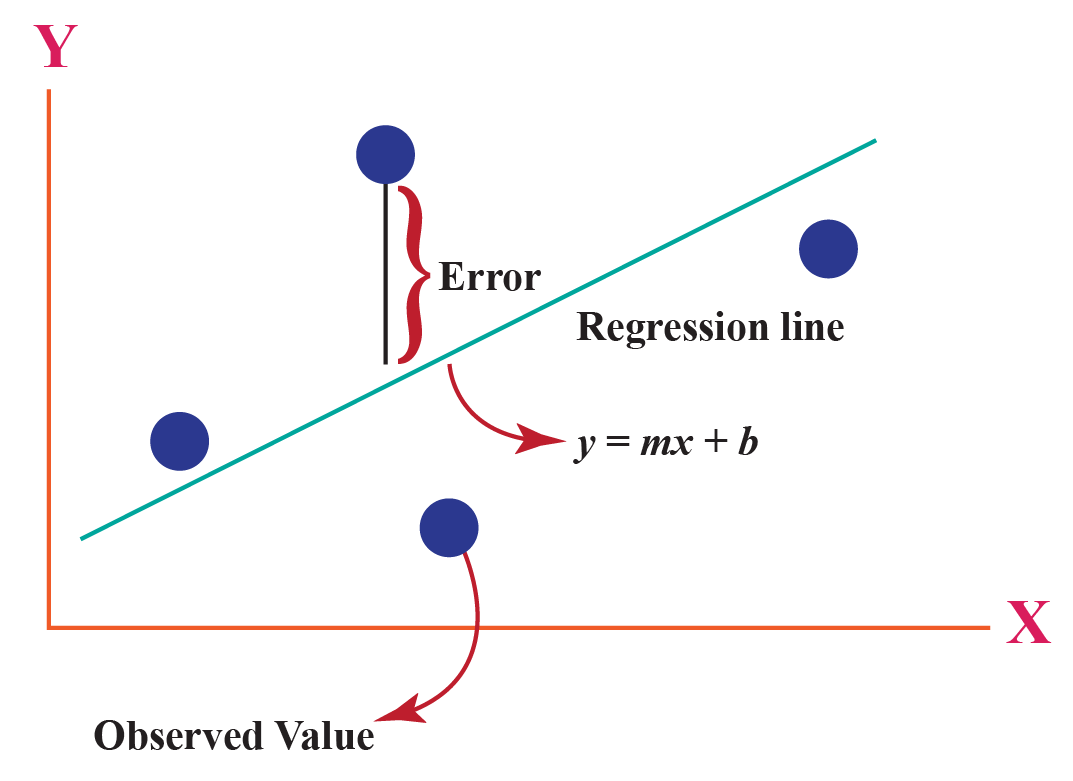
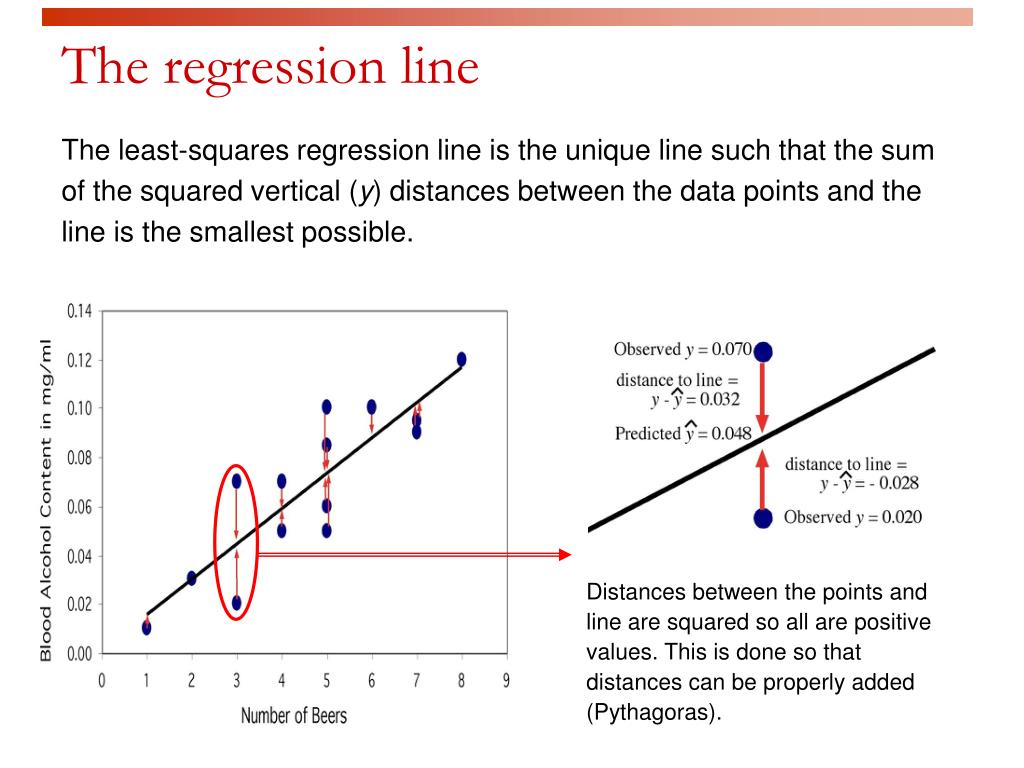
The procedure fits the line to the data points in a way that minimizes the sum of the squared vertical distances between the line and the points. The equation of the best fitting line is: We just need to find the values b 0 and b 1 which make the sum of the squared prediction errors the smallest they can be.

First, let’s create the following. The least squares method is a form of mathematical regression analysis used to determine the line of best fit for a. Our example will use the following ordered pairs:

The method of least squares is a method we can use to find the regression line that best fits a given dataset. To identify the least squares line from summary statistics: What is the least squares method?

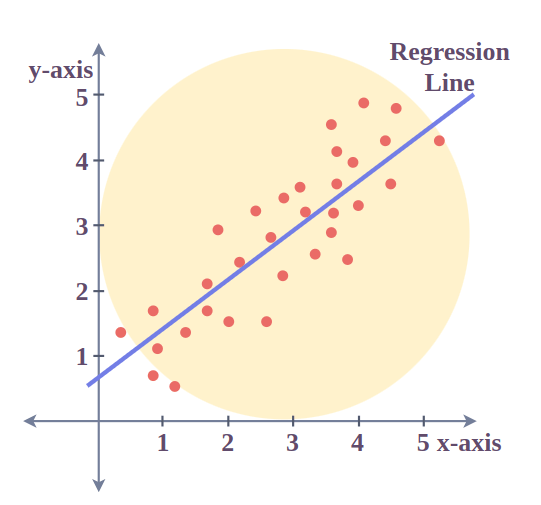
A least squares regression line represents the relationship between variables in a scatterplot. Line of best fit. Describing linear relationships with correlation;

Let us have a look at how the data points and the line of best fit obtained from the least squares method look when plotted on a graph. Anomalies are values that are too good, or bad, to be true or that represent rare cases. Statisticians typically use the least squares method (sometimes known as ordinary least squares, or ols) to arrive at the geometric equation for the line, either through manual.

Any other line you might choose would have a higher sse than the best fit line. However, i'm confused because i'm given four vectors. The equation of the best fitting line is:

First, look at your ordered pairs and find the mean of all of the x values and all of the y values. The line of best fit is calculated using the least squares method, which minimizes the sum of the squares of the vertical distances between the observed data points and the line. (−6, −1), (−2, 2), (1, 1), (7, 6) ( − 6, − 1), ( − 2, 2), ( 1, 1), ( 7, 6) i'm attempting to use the least squares approximation formulation that is as follows: