Outrageous Info About What Makes A Smooth Curve Graph In Excel

But essentially, the combination of that and np.linspace generates a.

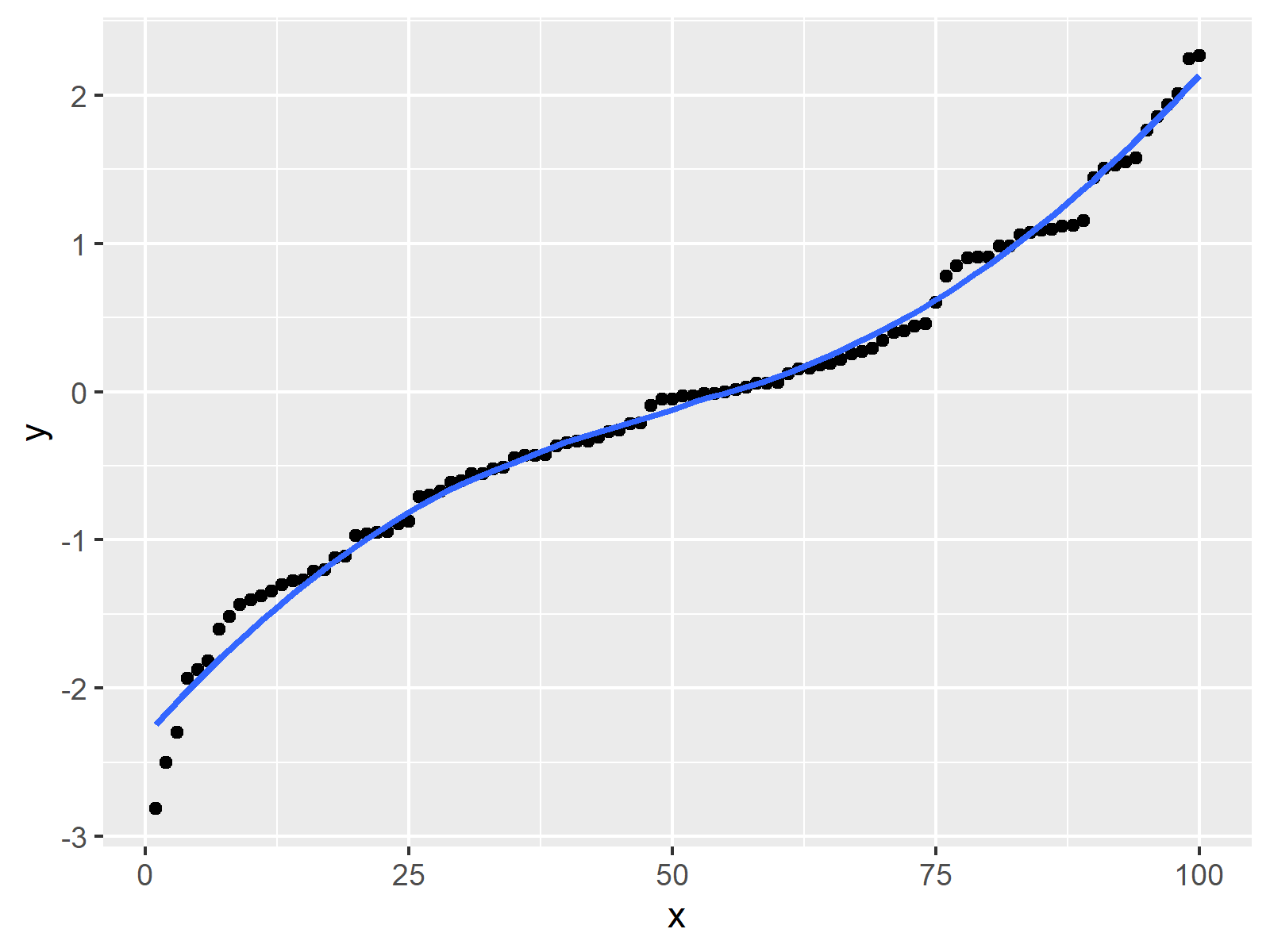
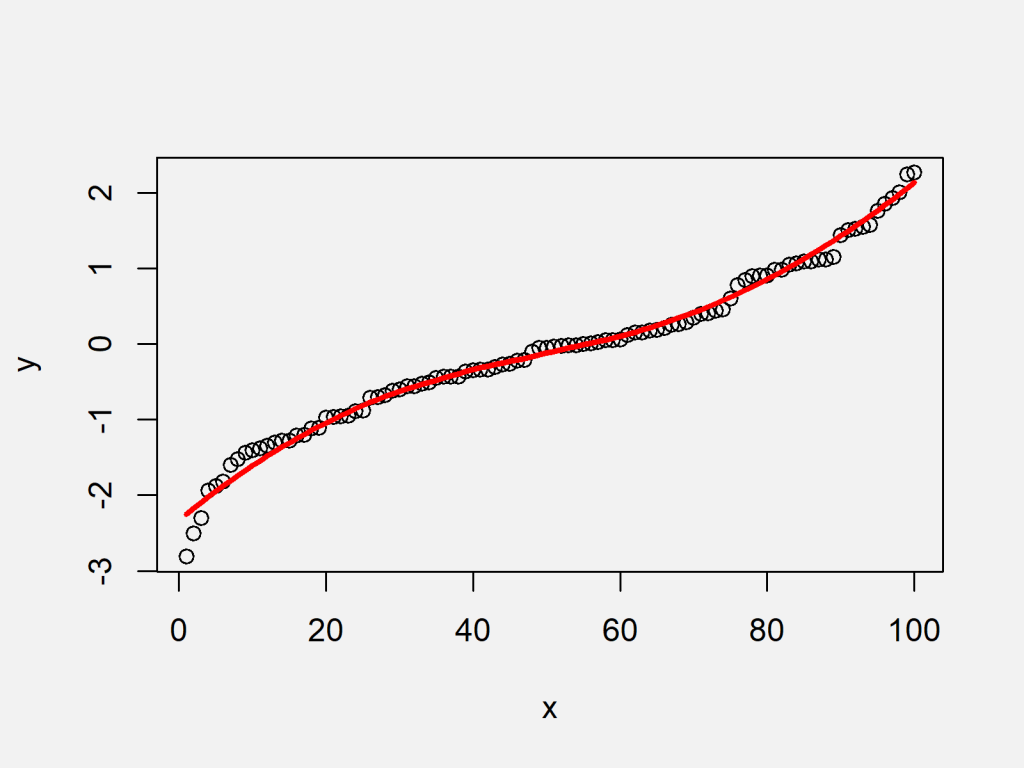
What makes a smooth curve. Smoothing is a very powerful technique used all across data analysis. In particular, a smooth curve is a. Starting in r2017a, you can smooth noisy data using built in matlab functionality:

It is designed to detect trends. In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to. You should instead use the original confidence values, otherwise you will get only 1.

If it is geometry, 'smooth' often means c∞ c ∞. Other names given to this technique are curve fitting and low pass filtering. A parabola, one of the simplest curves, after (straight) lines.

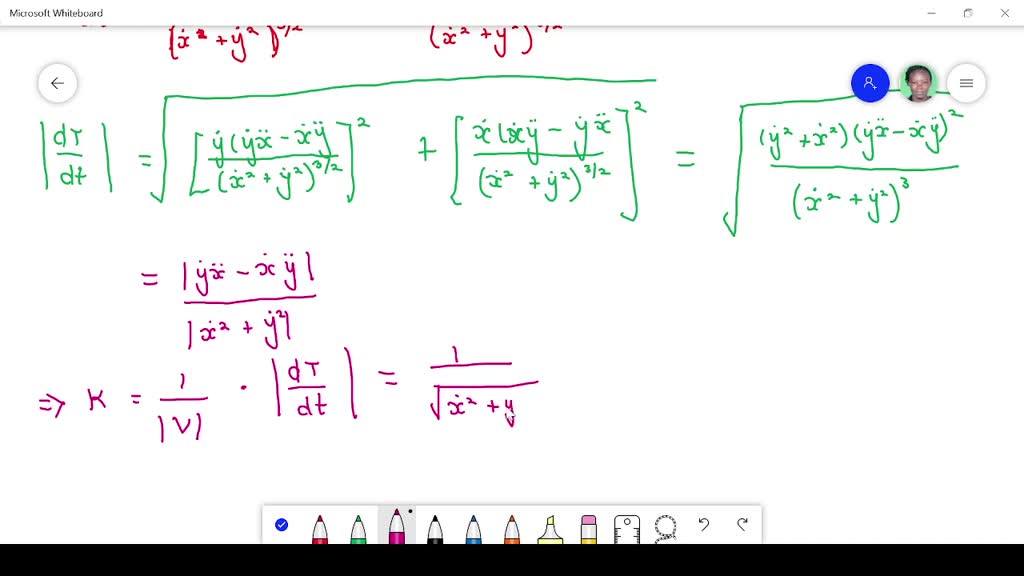
In single variable calculus (at georgetown), i was taught that a smooth curve is one which has all of the following: A curve $\mathbf{r}(t)$ is considered to be smooth if its derivative, $\mathbf{r}'(t)$, is continuous and nonzero for all values of $t$. Suppose the curve is defined by the parametric equations.

F(x1,., xm) = (f1(x1,.,xm) ,., fn(x1,.,xm)) from an open set in one euclidean space into another euclidean space is said to be smooth (or of class c∞) if it. (x, y, z) = (f(t), g(t), h(t)) ( x, y, z) = ( f ( t), g ( t), h ( t)), where t ∈ [a, b] t ∈ [ a, b] the curve is a smooth. A curve is said to be smooth if it has no singular points, in other words if it has a (unique) tangent at all points.

A smooth curve is a curve which is a smooth function, where the word curve is interpreted in the analytic geometry context. For this, one has to clarify whether the curve is considered in the. Consider the following curve in the plane, $(x(t),y(t))$, this curve is called smooth if the functions $x(t)$ and $y(t)$ are smooth, which simply means that for all $n$, the derivatives $\frac{d^nx}{dt^n}$ and $\frac{d^ny}{dt^n}$ exist.

My logic says yes because one can break it into a finite number of smooth. If you do a little search for scipy.interpolate.make_interp_spline, you can find more info on what that does. A clear definition of smoothing of a 1d signal from scipy cookbook shows you how it works.