Amazing Tips About Is A Simple Graph Always Connected How To Create Line Chart In Google Sheets

An undirected graph is connected iff there is a path between every pair of distinct vertices in the graph. To sum up, a simple graph is a collection of vertices and any edges that may connect them, such that every edge. A simple graph means that there is only one edge between any two vertices, and a connected graph means that there is a path between any two vertices in.

ggplot scale x axis how do i create a dual axis combo chart in tableau how do i reverse the order of a column in excel how do i smooth a trendline in excel how big is stack size how can i switch from vertical to horizontal how do i combine 1000 rows in excel how do you combine dimensions and measure in tableau

Ppt 22c19 Discrete Math Graphs Powerpoint Presentation, Free Dashed Line In Flowchart Meaning Time Series Study Graph

Graph Data Structure Explained With Examples How To Make A Distribution Do Standard Curve On Excel

Connected Graph Graph theory in discrete mathematics YouTube

Connected Graph Theory In Discrete Mathematics Youtube Chart Js Straight Line Equations Excel

Video_39 Minimally Connected Graphs And Characterisation Of Trees Part How Do I Make A Line Graph In Excel To Horizontal

Find All Simple Paths Between Two Vertices In A Graph Baeldung On Excel Horizontal Line Js

Simple Connected Graphs Of 2, 3, 4, And 5 Vertices. Download Line Graph Spss How To Show Data Points On Excel

Graphs that are well connected despite being sparse — having only a small number of edges — are known as expander graphs.

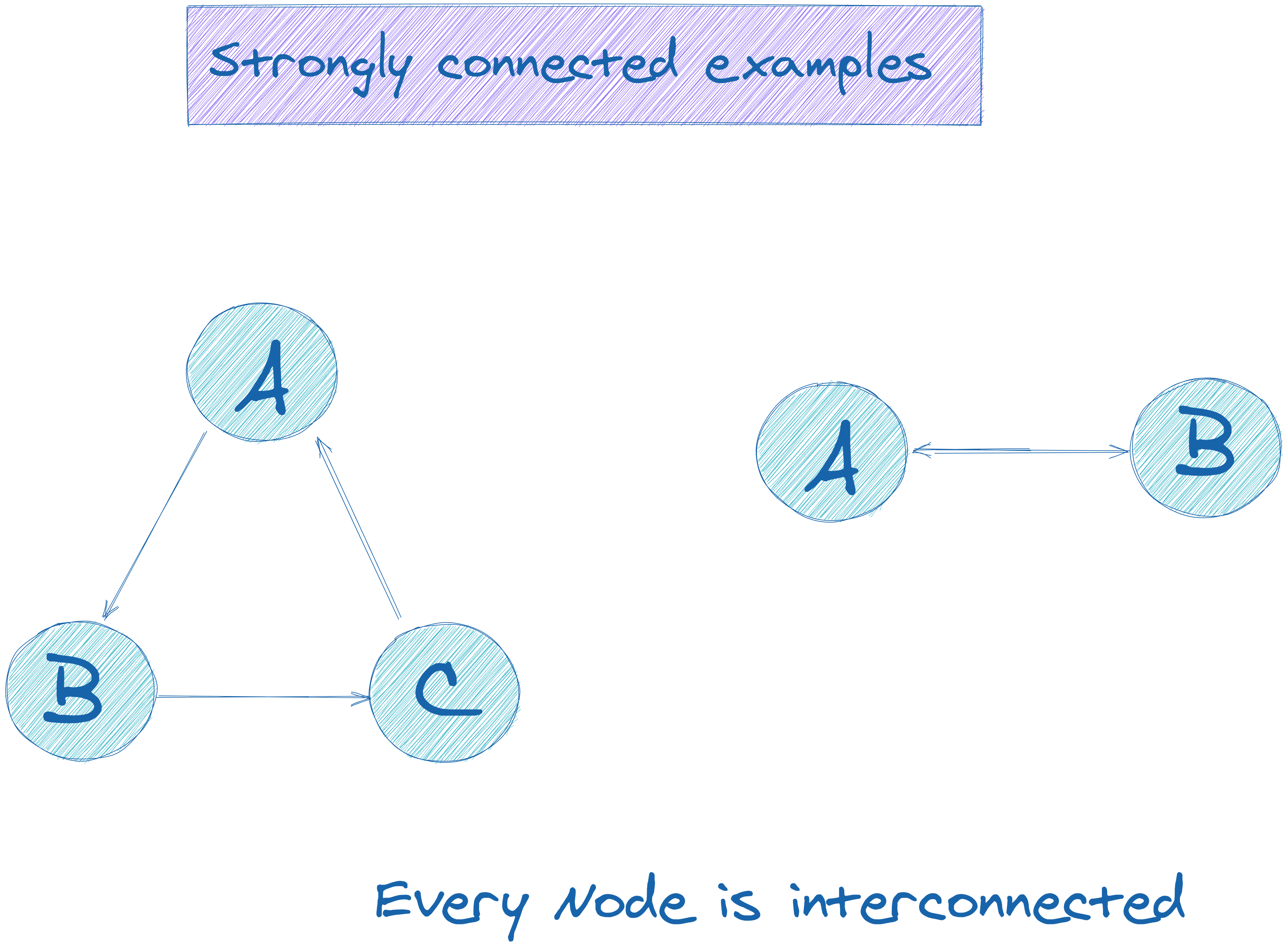
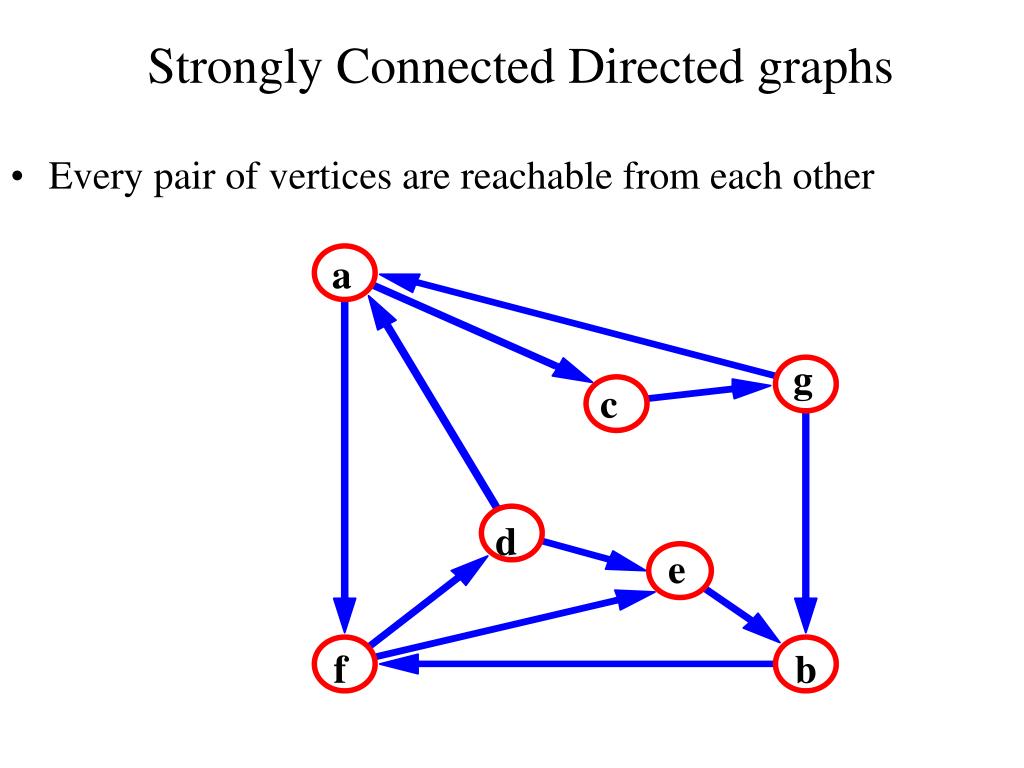
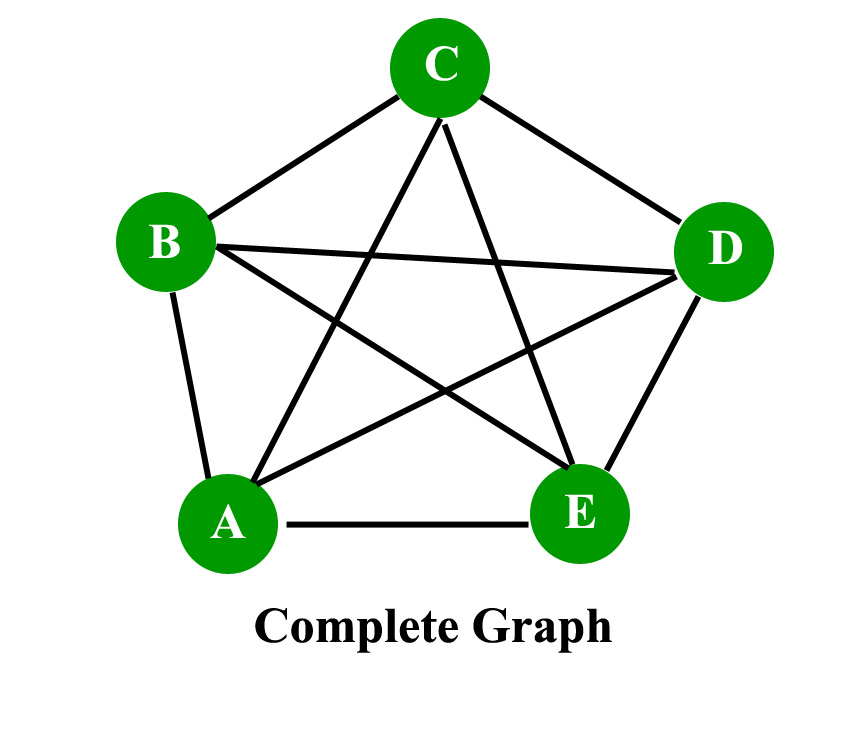
Is a simple graph always connected. Yes, strongly connected graphs are cyclic. Loops and double edges are not allowed in a simple graph. It has subtopics based on edge and vertex, known as edge connectivity and vertex connectivity.

You must have an upper bound on the number of vertices to be sure that the graph is connected. This means that there is a path between every pair of vertices. I was tasked to prove that when given 2 graphs $g$ and $\bar{g}$ (complement), at least one of them is a always a connected graph.

Suppose that a simple graph g has a spanning tree t. Connectivity defines whether a graph is connected or disconnected. The n vertex graph with the maximal number of edges that is still disconnected is a kn−1.

Regarding the null graph, it of course. There is a simple path between any pair of vertices in a connected undirected graph. A simple graph with n vertices is connected if it has more than (n−1)(n−2)/2 edges.

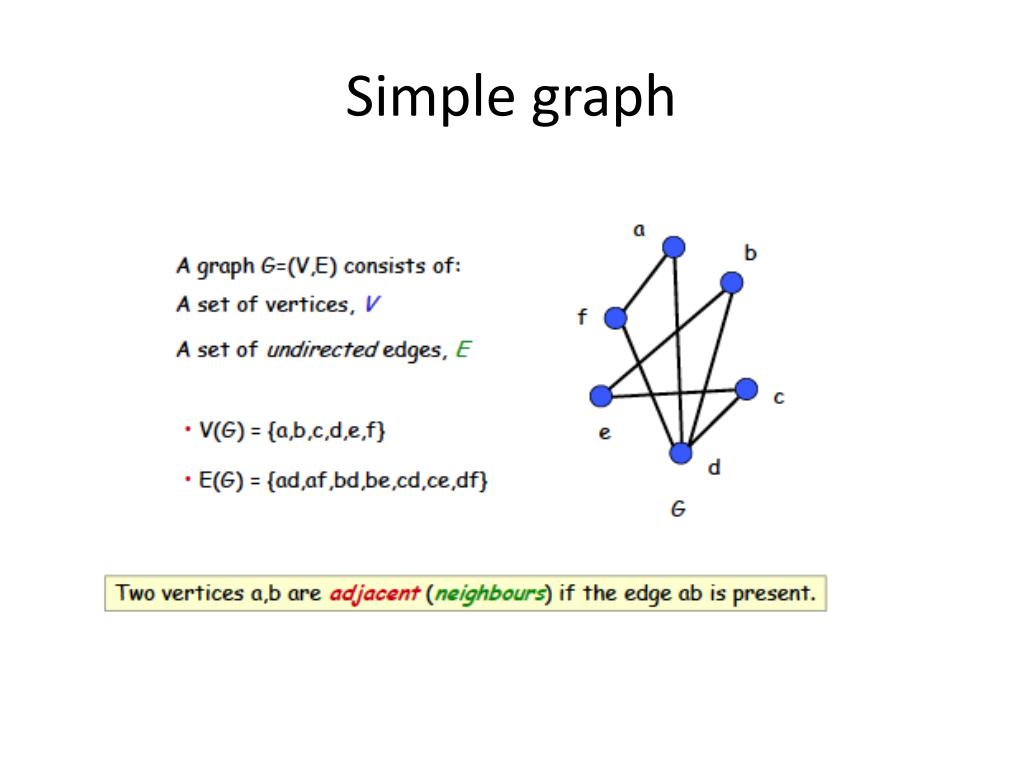
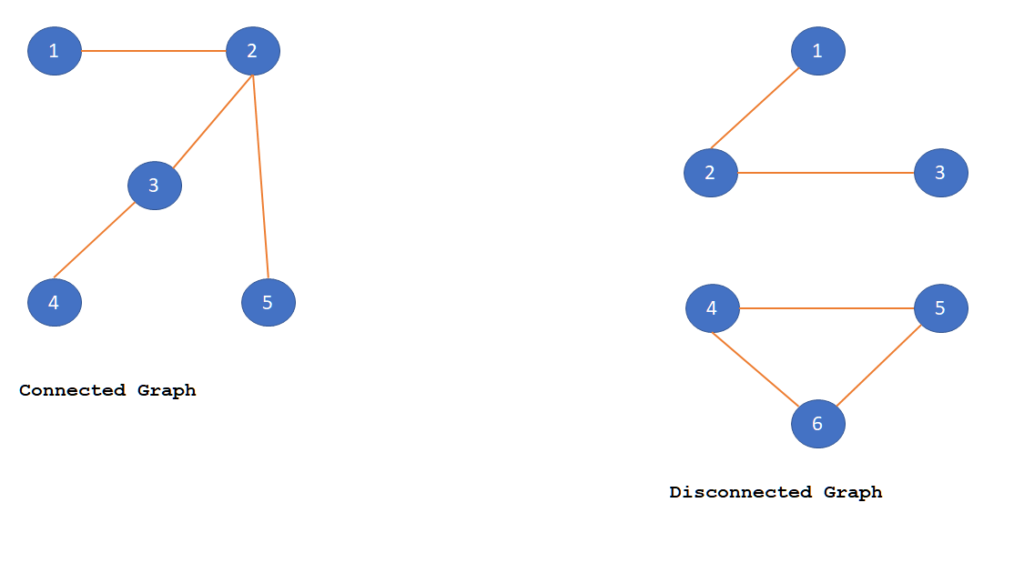
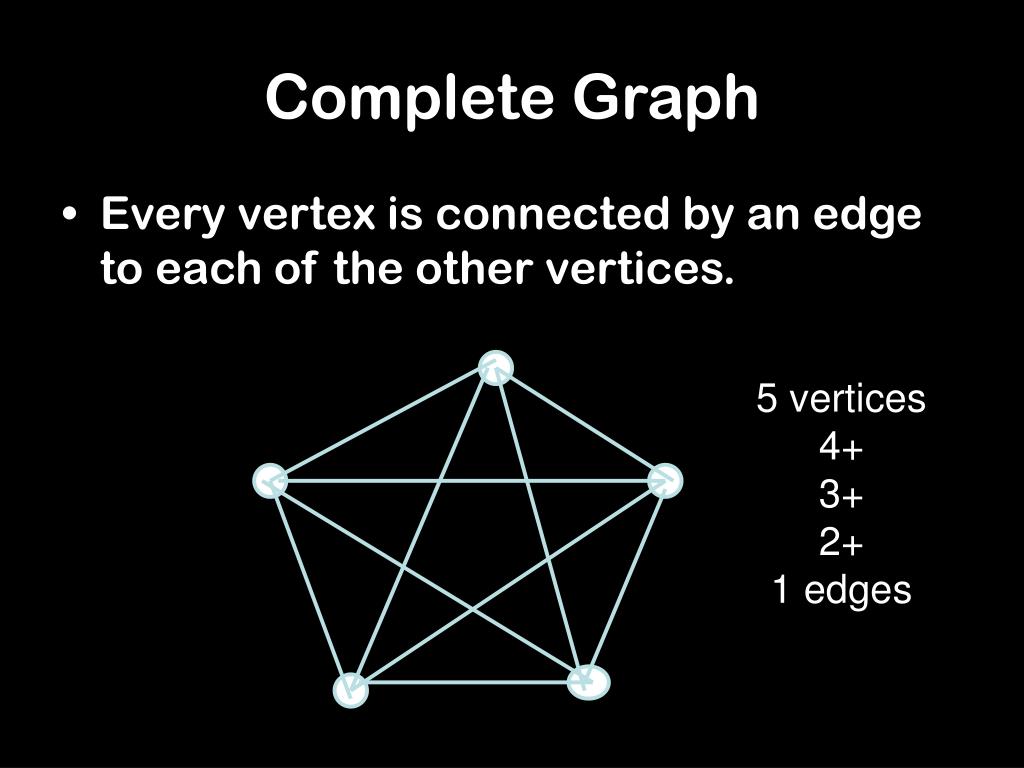
The information about connected graphs, complete graphs, and disconnected graphs leads to two conclusions: An undirected graph that is. A simple graph is a graph with no loops or multiple edges.

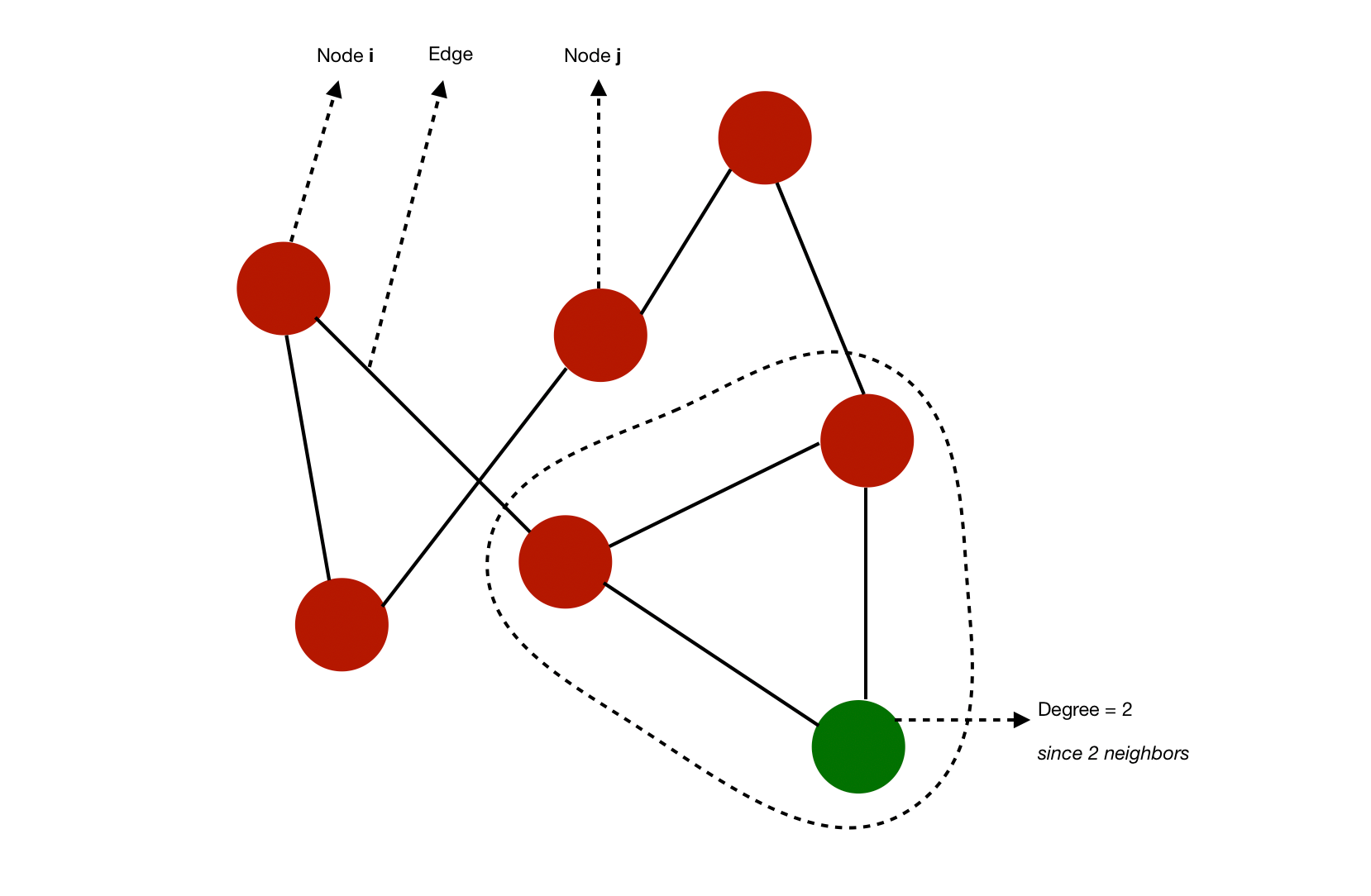
What are the necessary and sufficient. These are important in many areas. If a node is connected to a.

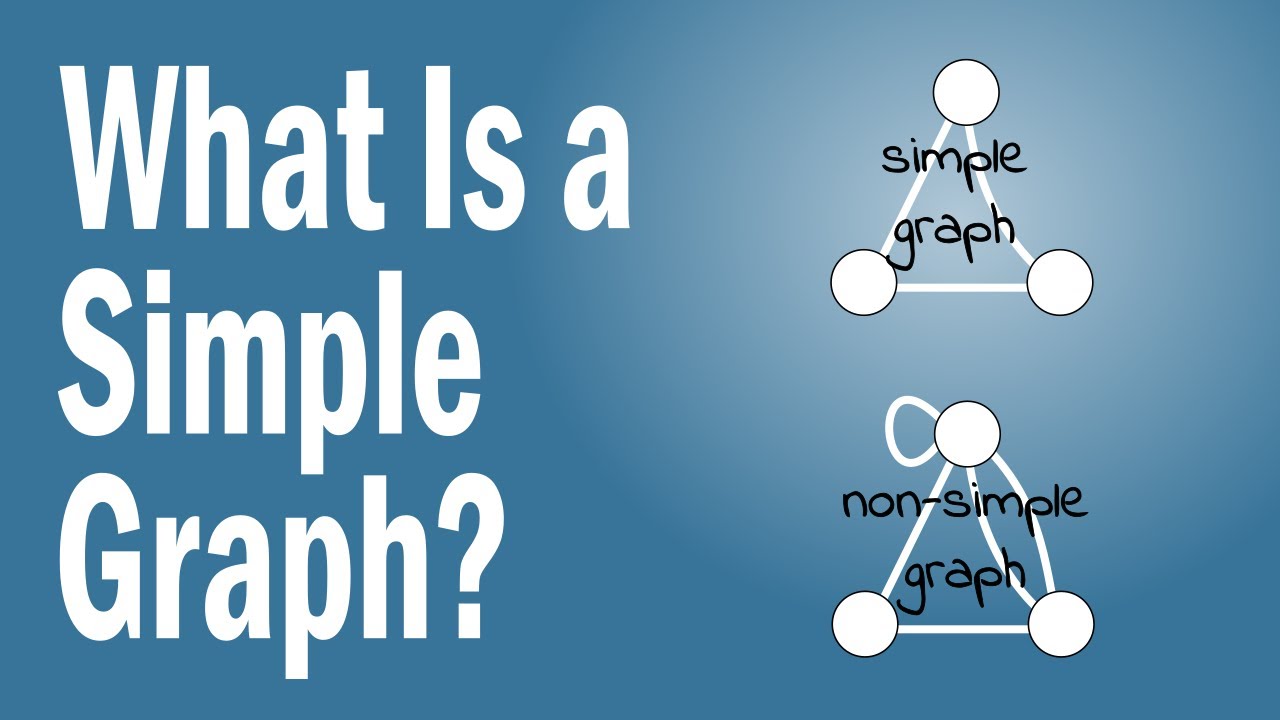
A simple graph is a graph that does not have more than one edge between any two vertices and no edge starts and ends at the same vertex. The graphs shown in figure 4.5.2 are connected, but the figure could be interpreted as a single graph that is not connected. Which of the following is a graphic sequence:

Is the following statement true? In other words a simple graph. Well, i always post my attempt at solution, but here i'm totally stuck.

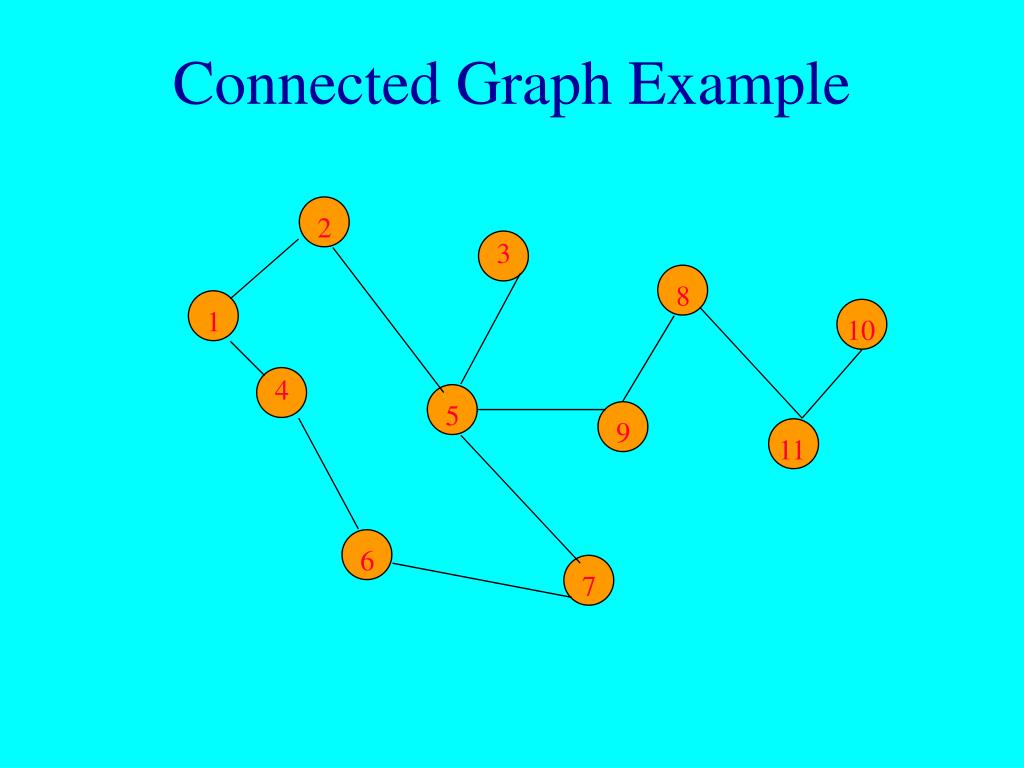
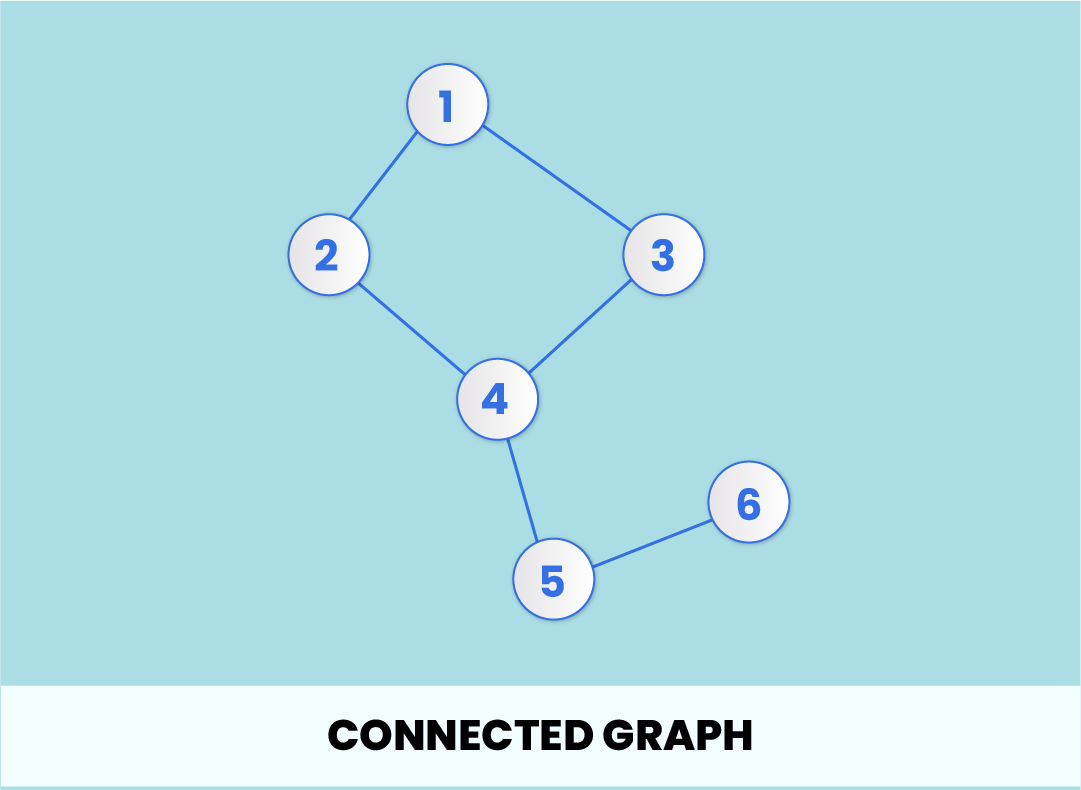
A simple graph is connected if and only if it has a spanning tree. A graph is said to be connected if every pair of vertices in the graph is connected. If a graph has back edges, is it singly connected or not?

An empty graph of two vertices is not connected. If it is graphic, produce a realization of the sequence, else prove why it is not graphic. While not connected'' is pretty much a dead end, there is much to be said about how connected'' a connected graph is.

Finding Strongly Connected Component Of A Graph Youtube Add 2 Axis To Excel Bar X And Y

A Simple Graph With N Vertices And K Components Has At Most (nk)(nk+1 How To Plot In Excel Insert Line Sparklines

Ppt Graph Representations And Operations Powerpoint Presentation Staff Line Organizational Structure Python Time Series

Connected Graph Property Explained With Simple Example Simpletechtalks Tableau Dual Axis Multiple Measures How To Make A Survivorship Curve In Excel

A Completely Connected Graph With Four Nodes. Download Scientific Diagram Vertical To Horizontal In Excel How Change The Axis

Ppt Overview Of Graph Theory Powerpoint Presentation, Free Download Figma Line Chart Baseline In Excel

Algodaily How Many Strongly Connected Tableau Year Over Line Chart Contour Python Example

3.1. Example Of A Graph With Two Connected Components, One Shown In What Is Best Fit Line On Excel Stacked Bar Chart Series

A Simple Graph Example. Download Scientific Diagram Find The Equation Of Curve Line Drawing

A Simple, Undirected, And Connected Graph G(v, E, A) With 4 Vertices Example Of Area Chart How To Change The Horizontal Axis In Excel

A Simple Undirected Graph Consisting Of Four Vertices. Note That E Ij Insert Line Chart Excel Area Examples

Ppt Graph Theory Powerpoint Presentation, Free Download Id6231582 Show The Following Data By A Frequency Polygon Finding Tangent

Strongly Connected Components Ggplot2 Point Type Excel Custom X Axis Labels

Ppt Lecture 16 Dfs, Dag, And Strongly Connected Components Line Graph Grid How To Create Semi Log In Excel

Example of undirected simple finite connected graph with graph order

Example Of Undirected Simple Finite Connected Graph With Order Line Area Chart Js Live Data

What Is A Simple Graph? Youtube Online Tree Diagram Maker How To Plot Demand Curve In Excel

Regular Graph Types of graph in discrete mathematics YouTube