Ideal Info About Can A Curved Graph Be Proportional Indifference Curve Excel

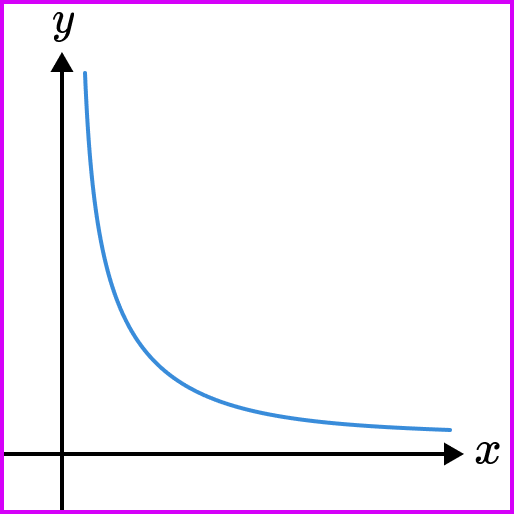
If i wanted to represent the graph of xy = x y = constant, why does the graph of xy = x y = constant come out to be a curve , something like this ?

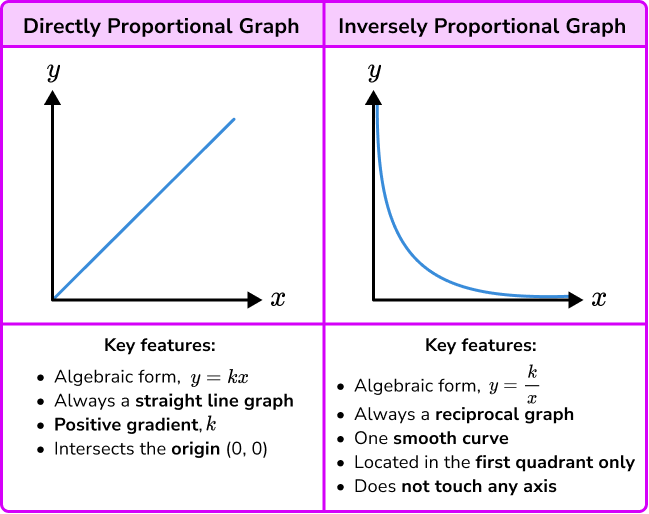
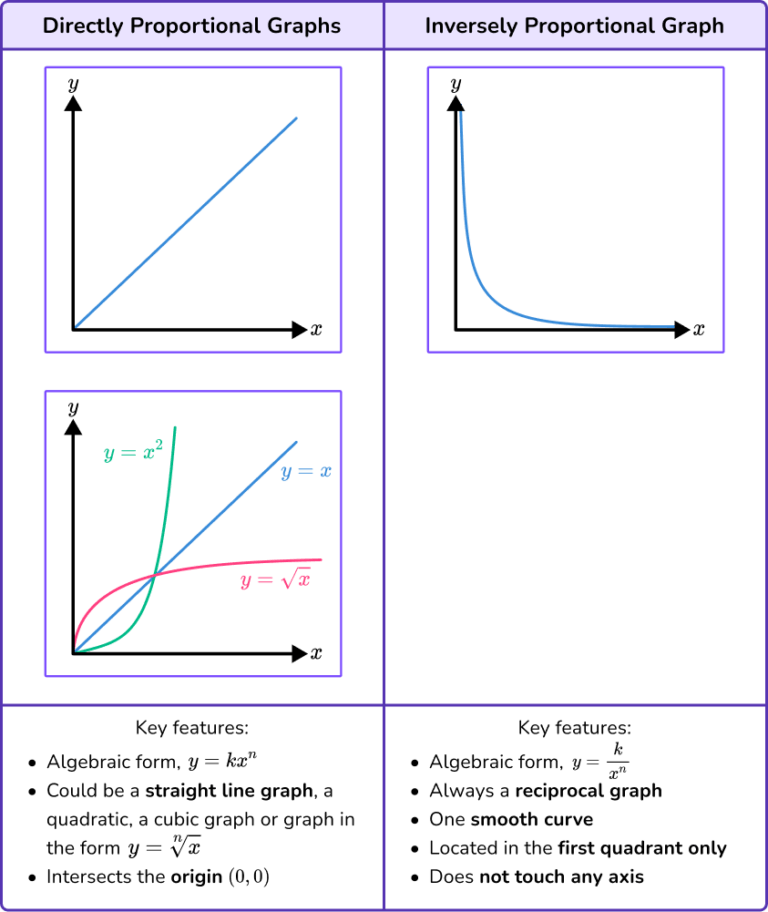
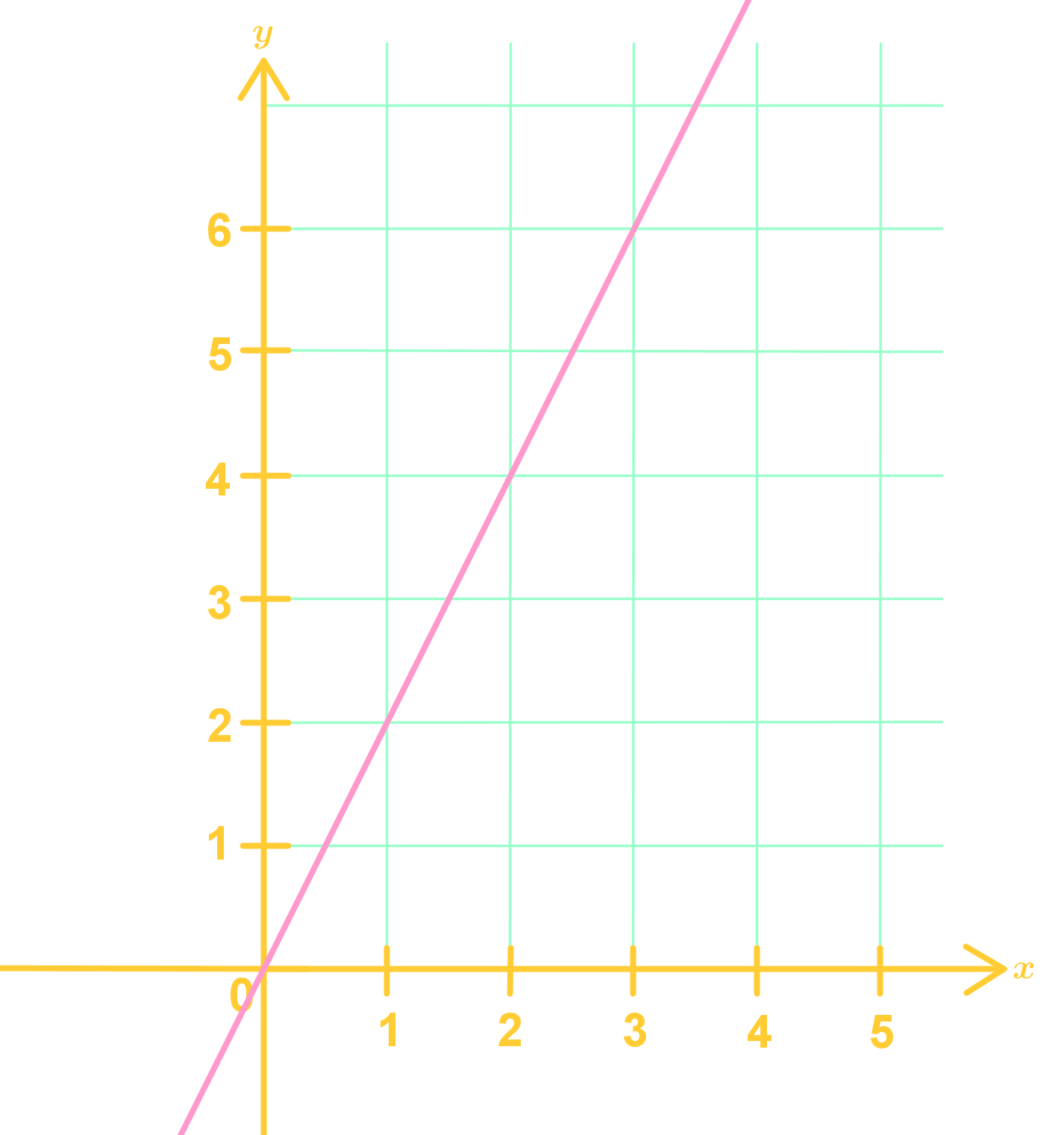
Can a curved graph be proportional. A linear relationship can be a proportional one (for example y=3x is proportional), but usually a linear equation has a proportional component plus some constant number (for example y=3x +4). It should be a linear relationship between the two variables. Direct proportion creates a linear graph where k is the gradient.

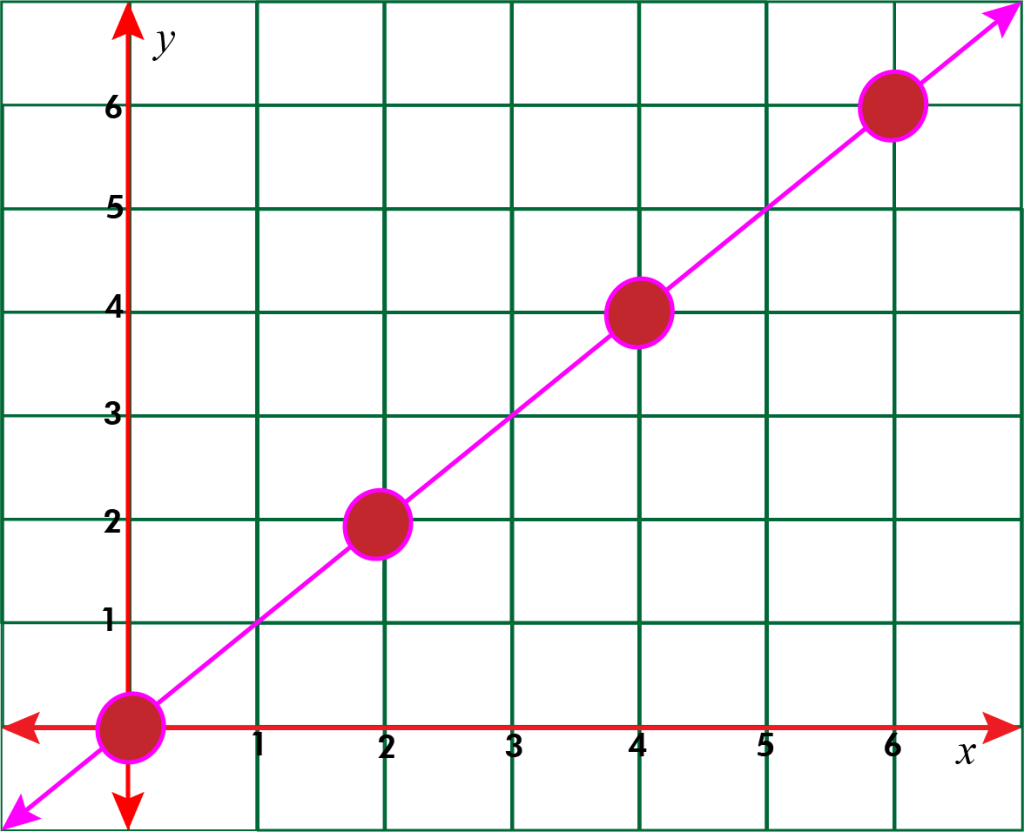
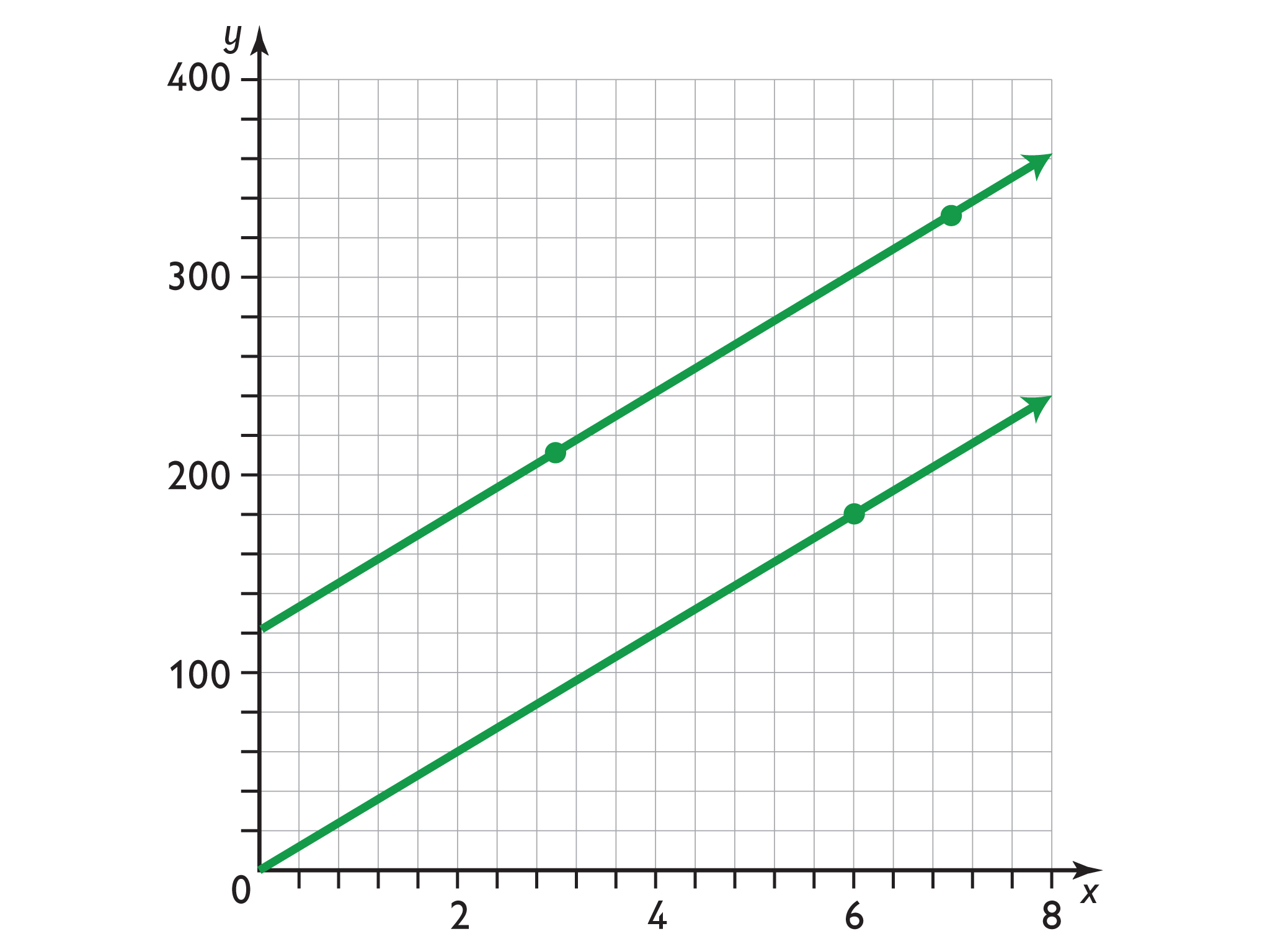
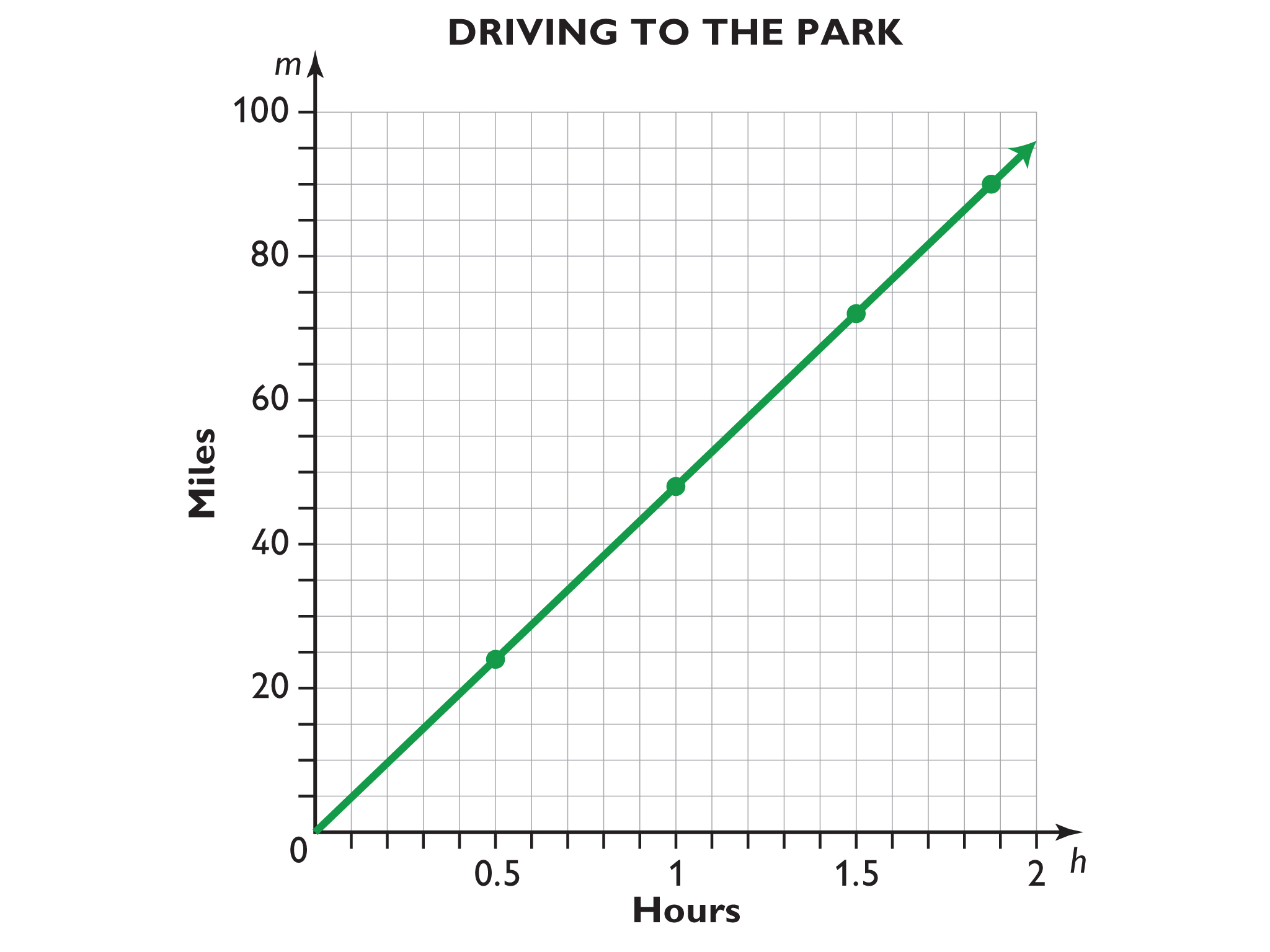
The line that they lie on passes through the origin, \((0,0)\). If the graph is a straight line through the origin, then it represents a proportional relationship. This means that for any increase or decrease in one variable, there will be a corresponding increase or decrease in the other variable that keeps the ratio the same.

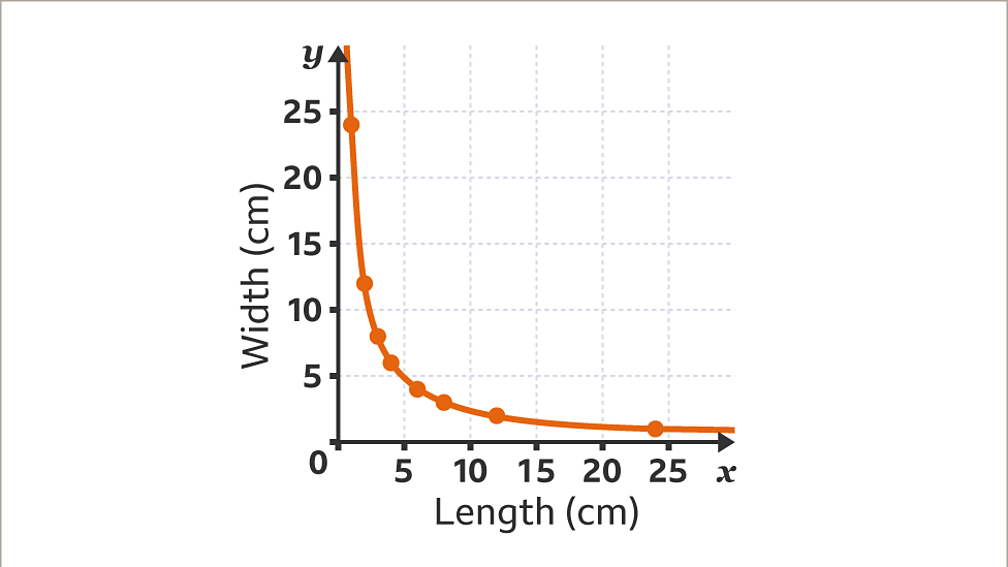
Modified 6 years, 5 months ago. In our example, when x increases, y increases three times as much. An inverse proportional graph requires more points to give an accurate curve.

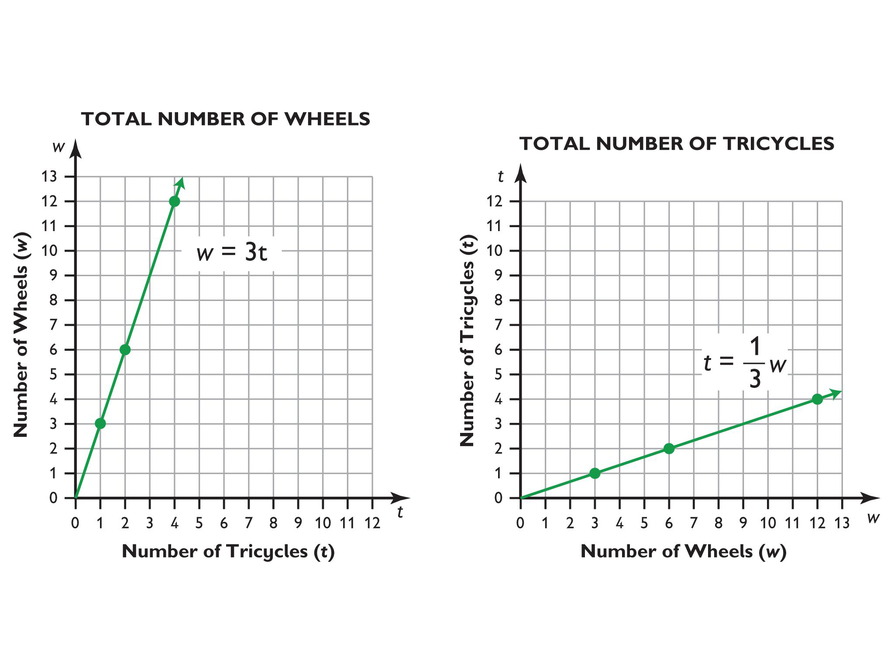
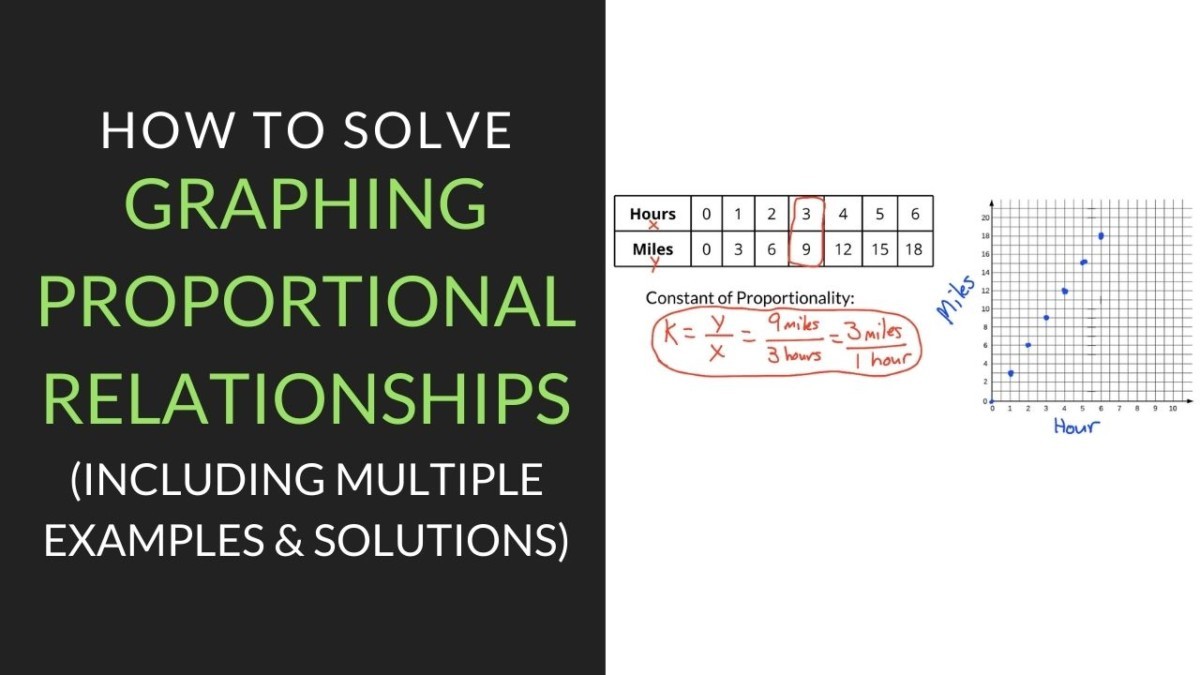
Actually, x = 5y x = 5 y. Proportional lines are straight lines on a graph that start at the origin also linear lines are defined by the equation y = mx + b proportional lines are defined by the equation y = kx A graph and table can both represent proportional relationships.

Asked 6 years, 5 months ago. X = −5y x = − 5 y. This is a curved line.

The bar graph by default is set to d for daily. Inverse proportion can be represented graphically using 𝑦 =𝑎/𝑥. Want to join the conversation?

Graphs that represent proportional relationships all have a few things in common: We look for certain features of the graph and perform some test calculations to help us decide. The slider turns orange if the schedule does not meet your sleep goal.

When we graph this relationship we get a curved graph. Tap the days active and drag the curved slider to set bedtime and wake up times. This could mean the snail is traveling \(\frac{5}{4}\) feet per minute or that the recipe calls for \(1\frac{1}{4}\) cups of yogurt for every teaspoon of cinnamon.

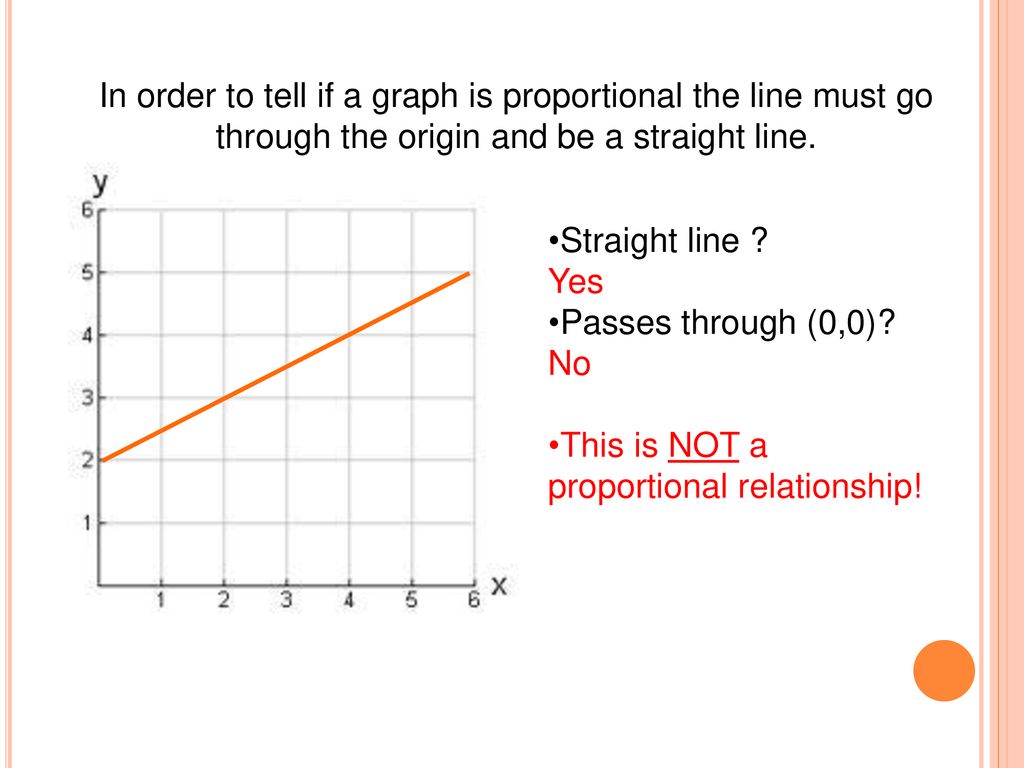
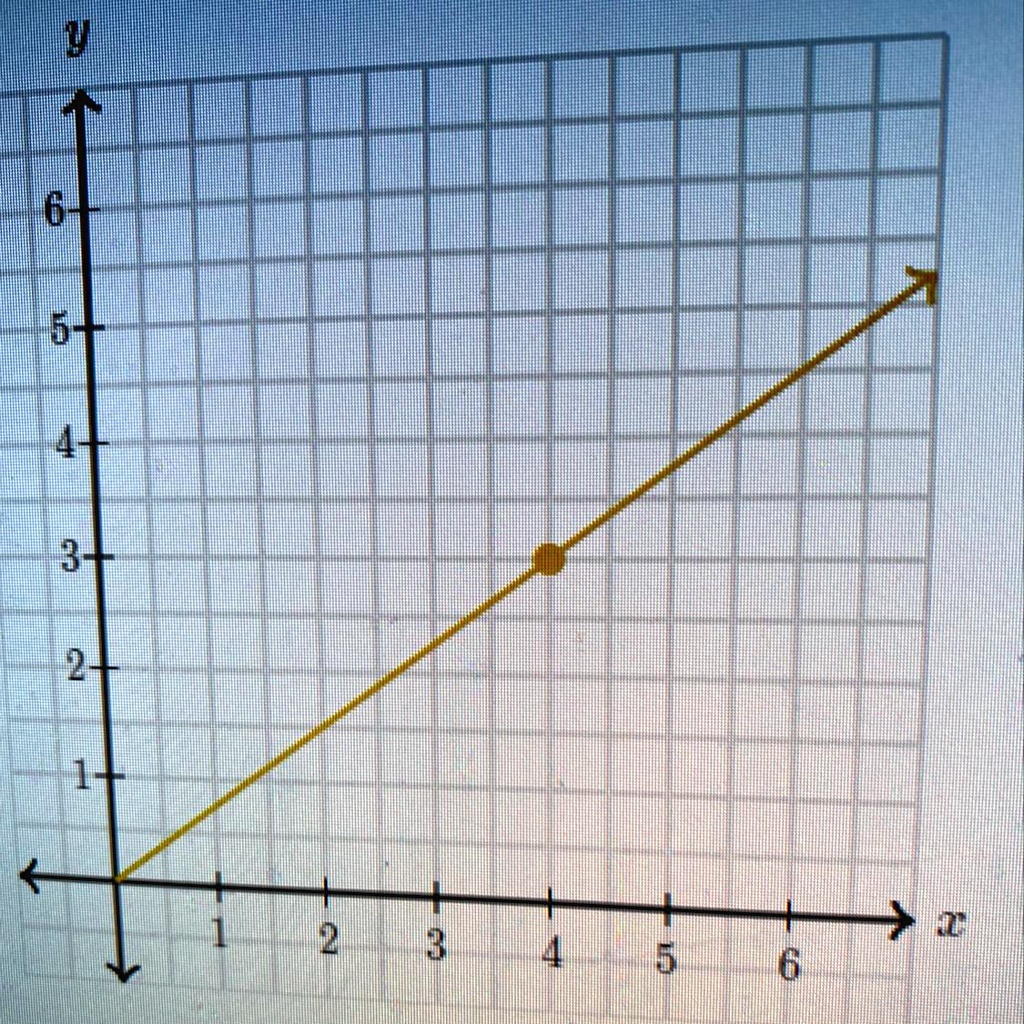
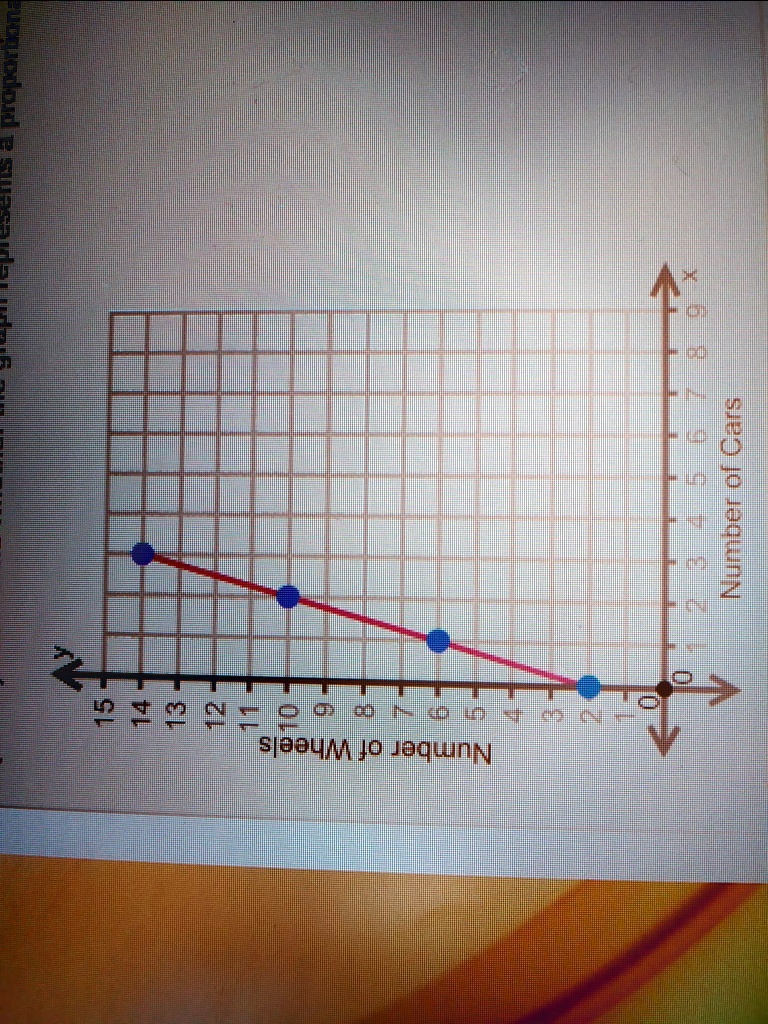
Both direct and inverse proportion can be represented graphically. So, our constant of proportionality is 3. Graph b is a straight line but does not go through the origin, so it does not represent a proportional relationship.

How do we know if a graph represents either direct or inverse proportionality? Here are some graphs that do not represent proportional relationships: Check whether the graph is a.