Who Else Wants Info About Do Curved Vectors Exist Excel Add Vertical Line To Scatter Plot
Differential geometry of curves and surfaces, do carmo (chapter 1) definition:
Do curved vectors exist. So, a vector is a basic building block, and shouldn't be too broadly defined. If $u$ is convex, then there exists a vector field. One of my weak spots are the smooth and curved shapes.
Is the vector attached to some object? A parameterized differentiable curve is. Parameterized differentiable curve is a differentiable map α:
A vector \(\vecs v\) is tangent to the graph. Suppose $\bfg$ is a $c^1$ vector field in an open set $u\subset \r^3$ such that $\operatorname{div}\bfg = 0$. In the two dimensional plane, a vector eld f (x;
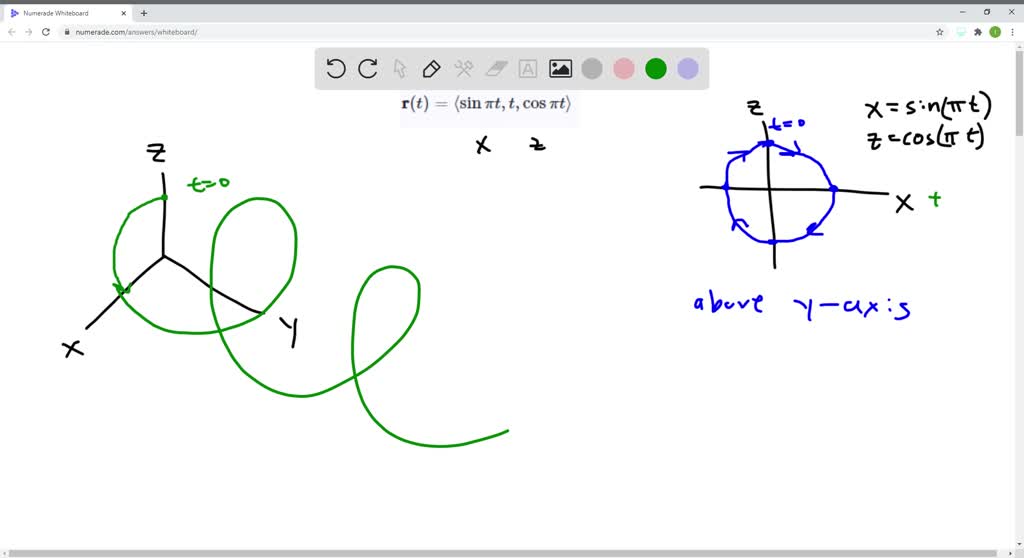
Here we ask a sort of “inverse” question. Circle circles curves sphere spheres. I → r3 of an interval i = (a,b) of the real line r into r3.
Do curves, circles and spheres really exist? For this paper i wanted to be able to find the point in space on a curved line, for instance a circle. Divergence and curl of vector elds.
The curl of f is de ned. Well, a short answer is that we use vectors to do linear algebra and geometry, and we use limits and calculus to apply those concepts to curved objects. Normally, i use various tools to do that:
Like does it not matter where the 'tail' is. Recognize parametric equations for a space curve. Normal vector of a curve.
In three dimensions, as in two, vectors are commonly expressed in component form, \(\vecs v= x,y,z \), or in terms of the standard unit vectors, \(\vecs v= x\,\mathbf{\hat. Deriving the equation of geodesic deviation one looks at two test masses on positions $x^\mu$ und $\tilde{x}^\mu$ and defines the separation vector. This question arose mainly when i was learning about plotting.
A function from an interval into some space) or as a set of points (typically the. A unit normal vector of a curve, by its definition, is perpendicular to the curve at given point. Given a function \(f\) or a vector field \(\bff\), we can easily compute \(\nabla f\) or \(\curl \bff\).
It really depends on whether you're thinking of a curve as a parametrized curve (i.e. As i understand it, the curl of a vector field generates another field where each vector is orthogonal to the plane of rotation in the original field, and the divergence. This means a normal vector of a curve at a given point is.